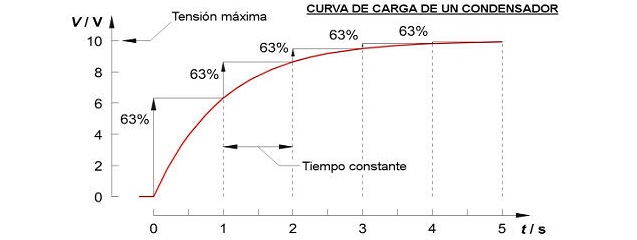
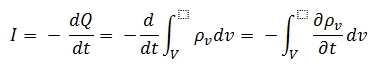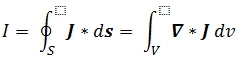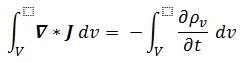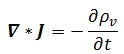Cuando pensamos en la carga o descarga de un condensador rápidamente imaginamos una curva exponencial que relaciona la tensión (V) con el tiempo (t). Es uno de los primeros conceptos que nos explican cuando estudiamos un curso de electrónica.
Al comenzar el estudio de una materia, de la que no tenemos conocimientos previos, es habitual que memoricemos muchos conceptos sin razonarlos, para sentar de forma rápida una base que nos permita avanzar en el estudio. Cuando ya tenemos cierta soltura con la asignatura pocas veces volvemos atrás para razonar aquellos conceptos que ya damos por entendidos.
En las siguientes líneas vamos a demostrar de forma analítica a que se debe que la carga (o descarga) de un condensador sea exponencial en lugar de lineal, que a priori podría parecer más lógico.
Sabemos que la corriente eléctrica (I) es la variación de carga (Q) que se produce en el circuito respecto al tiempo (t). Como el sentido de la corriente es inverso al sentido del movimiento de los electrones en nuestro circuito, podemos definir matemáticamente:
Donde rho es la densidad de carga en el volumen de conductor que estamos analizando. Al introducir la deriva dentro de la integral pasa a ser parcial ya que la densidad de carga podría depender del tiempo y la posición.
Por otra parte podemos definir la corriente eléctrica (I), que es una magnitud macroscópica, como la suma (integral) de todos los elementos (vectoriales) de corriente (J) que atraviesan a nivel microscópico una superficie de conductor. A continuación aplicaré el teorema de la divergencia para transformar la integral de superficie a una integral del volumen encerrado por dicha superficie.
Donde el gradiende de J representa el flujo neto de elementos (vectoriales) de corriente que entran o salen del volumen estudiado, es decir, el incremento o decremento de carga que se está produciendo en la densidad de corriente.
No tenemos que olvidar que la situación que estamos analizando no es una situación donde la corriente permanece constante, ya que en ese caso la corriente que entra al volumen de estudio sería igual a la que sale, siendo el gradiende de J igual a cero. Estamos analizando una situación transitoria donde el flujo de entrada es superior al de salida (carga) o el flujo de entrada es inferior al de salida (descarga).
Igualando ambos resultados de I, tenemos:
Como era de esperar la variación del flujo neto de elementos (vectoriales) de carga es igual a las variaciones de carga en sentido contrario. Esta ecuación vectorial define la continuidad de carga, evidentemente cumple con el principio de conservación de carga, y de ella se deduce la ley de Kirchhoff.
SEAS es el centro de formación online del Grupo San Valero, especializado en el ámbito técnico, industrial y de empresa. Visita www.seas.es para consultar nuestra oferta formativa de cursos y másteres. Formación profesional para el empleo de calidad y accesible para todos.